How to use chi-square to test an inheritance pattern
- Jolene Pappas
- Feb 22, 2019
- 5 min read
Updated: Jan 15, 2024
Would you rather watch a video than read? Here is a video version of this post:
Many biology classes use the chi-squared statistical test during heredity units. Chi-square can help determine the inheritance pattern of a trait by statistically comparing the predicted outcomes with the actual data. The variables for a chi-square calculation are expected (e) and observed (o) values. The observed values come from collected data, while expected values are based on the predicted frequencies (which students often learn to find from Punnett squares).
This example will use chi-square to check if a hypothesized inheritance pattern appears to be correct. The term “inheritance pattern” describes how genotypes lead to phenotypes for a trait. For example, a trait with an autosomal dominant inheritance pattern is determined by a single gene that is not located on a sex chromosome (autosomal), and only one copy of the allele for the trait is necessary to produce the trait’s phenotype (dominant).
This example uses data from the Heredity I: Eye Color and Tails simulation. We are examining a white-eye trait in a fictional organism. We need to select a cross where one individual has white eyes and the other has black eyes. The tails don't matter in this case, but it is easier if both parents either have a tail or both are tailless. The example used here starts with black eyed females and white eyed males. The first pair selected is called the P generation, and these are all assumed to be homozygous for whichever version of the trait they have.

The offspring of the P generation are the F1 generation. In this example, there are 56 black eye females and 60 black eye males in this F1 generation. Once the F1 data is recorded, select the F1 cross. The F1 cross is between members of the F1 generation.

The offspring of the F1 cross are the F2 generation. In the F2 generation there are 38 females with black eyes, 34 males with black eyes, 15 white eye females, and 17 white eye males.

To analyze the data, we'll first look at the F1 data. In this case, 100 % of the F1 generation has black eyes. Based on this, we’re going to hypothesize that this eye color gene is autosomal and that black eyes are dominant. The F2 data will be used to test this.

One question that students frequently ask is “Do I have to separate males and females?” If you don’t separate out the numbers for males and females, you may miss if a trait is X-linked. Of course, this assumes that the animal uses XY sex determination. Most mammals do use this method, in addition to fruit flies, which are a commonly used organism for genetic study (although the process is different in fruit flies than in mammals). However, many animals use different methods. Here's a video that introduces a few variations. For the most part when biology classes look at heredity, XY sex determination is the default method.
For the analysis, we’re going to represent the black eye allele with a 'B' and the white eye allele with a 'b'. The P generation individuals with black eyes have the genotype BB and the white eye individuals are bb. Each black eyed parent passes on the black allele (B) and each white eye parent passes on the white allele (b). All F1 individuals have one black eye allele and one white eye allele (Bb). We hypothesize that the black eye allele is dominant, so heterozygotes (Bb) will have the black eye phenotype.
To do the chi-squared test we need expected values for the F2 generation. To get the F2 expected, we cross the heterozygotes from the F1 generation. For this example, we’ll visualize the cross with a Punnett square. The Punnett square shows that we expect 75% of the F2 generation to have black eyes and 25% to have white eyes.

We hypothesize that the black/white eye color gene is autosomal (located on a chromosome that doesn't determine sex), so we expect an even split of males and females. To get the probability that an individual has black eyes and is female, we multiply the probability of an individual having black eyes by the probability of an individual being female. 75% x 50% is 37.5%, so we expect 37.5% of the F2 generation to be black eyed females. Remember that you can do this math in fractions (3/4 x 1/2 = 3/8) or frequencies (0.75 x 0.5 = .375) if you prefer. We expect 37.5% to be black eye males, 12.5% to be white eye females and 12.5% to be white eye males.

We will use these expected percentages (or frequencies/fractions) to find the expected value that will be used for the 'e' variable of the chi-squared equation. First, find the total number of individuals in the F2 generation by adding all of the F2 results. In this example, there are 104 individuals in the F2 generation. Then, multiply the expected percentages by the total. For the black eyed females, 104 x 37.5% is 39. This means we expect 39 individuals to be females with black eyes. In this example, the results are all whole numbers, but if you get an answer with a decimal, there isn't any need to round to whole numbers; just use the decimal for your chi-square calculations.

Now that we have calculated the expected values (e), we have all the variables we need for the chi-squared calculation. Remember that o represents the data collected from the F2 generation. When doing the chi-square calculation, use the corresponding observed and expected values for a category (black eyed females) together.
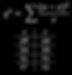

For the chi-square calculation, subtract the expected from the observed, square that, and then divide by the expected for each of the categories. This example has four categories; black eye females, black eye males, white eye females, and white eye males. After completing the calculation for each category, add the resulting values to get the chi-squared value. In this case, the chi-squared value is 2.2.
The critical value table helps us to interpret the chi-squared results. To find the critical value on the table we need to know two pieces of information; the degrees of freedom and the p-value.
The degrees of freedom is the number of categories minus 1. We have four categories, so there are three degrees of freedom. The p-value is the probability that the results could be due to chance. High school biology situations typically use a p-value of 0.05. Looking at the chi-square table, the 3 degrees of freedom column and the 0.05 p-value row give us a critical value of 7.82.

To interpret the results, compare the chi-square value to the critical value. If the chi-square value is greater than the critical value the hypothesis is rejected. This means that the observed values do not match the expected. If the Chi-square value is not greater than the critical value, then we fail to reject the hypothesis. Failing to reject the hypothesis means that there probably is not a difference between the observed and expected.
For this example, the chi-square value of 2.2 is less than the critical value of 7.82. Based on that, we do not reject the hypothesis. This means that our expected values are statistically equivalent to the values observed in the data. We conclude that the inheritance pattern we used to determine the F2 generation percentages is likely to be the correct interpretation. Our final conclusion is that the data is consistent with this eye color trait being determined by an autosomal gene and that the black eye allele is dominant and the white eye allele is recessive.